Practice Datasets

Below are various datasets from these readings and from lectures and exercises across our courses. For each one, there is a quick explanation of the study design which also details the research aims of the project.

Pick one of the datasets to test yourself with fitting, checking, interpreting, and reporting on multilevel models.

This dataset contains information on 900 children from 30 different schools across Scotland. The data was collected as part of a study looking at whether education-related motivation is associated with school grades. This is expected to be different for state vs privately funded schools.
All children completed an ‘education motivation’ questionnaire, and their end-of-year grade average has been recorded.

Data are available at https://uoepsy.github.io/data/schoolmot.csv.

variable description
motiv Child's Education Motivation Score (range 0 - 10)
funding Funding ('state' or 'private')
schoolid Name of School that the child attends
grade Child's end-of-year grade average (0-100) 
df <- read_csv("https://uoepsy.github.io/data/schoolmot.csv")

mod1 <- lmer(grade ~ motiv * funding + 
               (1 + motiv | schoolid), 
             data = df)

summary(mod1)

These data come from 112 people across 12 different Scottish dwellings (cities and towns). Information is captured on their ages and a measure of life satisfaction. The researchers are interested in if there is an association between age and life-satisfaction.

Data are available at https://uoepsy.github.io/data/lmm_lifesatscot.csv.

variable description
age Age (years)
lifesat Life Satisfaction score
dwelling Dwelling (town/city in Scotland)
size Size of Dwelling (> or <100k people) 
df <- read_csv("https://uoepsy.github.io/data/lmm_lifesatscot.csv")

mod <- lmer(lifesat ~ 1 + age + (1 + age | dwelling), df)

# if you want to see a cross-level interaction (not relevant for RQ):
df$age <- df$age/10 # makes fitting easier
mod2 <- lmer(lifesat ~ 1 + age * size + (1 + age | dwelling), df)

A questionnaire was sent to all UK civil service departments, and the lmm_jsup.csv dataset contains all responses that were received. Some of these departments work as hybrid or ‘virtual’ departments, with a mix of remote and office-based employees. Others are fully office-based.

The questionnaire included items asking about how much the respondent believe in the department and how it engages with the community, what it produces, how it operates and how treats its people. A composite measure of ‘workplace-pride’ was constructed for each employee. Employees in the civil service are categorised into 3 different roles: A, B and C. The roles tend to increase in responsibility, with role C being more managerial, and role A having less responsibility. We also have data on the length of time each employee has been in the department (sometimes new employees come straight in at role C, but many of them start in role A and work up over time).

We’re interested in whether the different roles are associated with differences in workplace-pride.

Data are available at https://uoepsy.github.io/data/lmm_jsup.csv.

variable description
department_name Name of government department
dept Department Acronym
virtual Whether the department functions as hybrid department with various employees working remotely (1), or as a fully in-person office (0)
role Employee role (A, B or C)
seniority Employees seniority point. These map to roles, such that role A is 0-4, role B is 5-9, role C is 10-14. Higher numbers indicate more seniority
employment_length Length of employment in the department (years)
wp Composite Measure of 'Workplace Pride' 
df <- read_csv("https://uoepsy.github.io/data/lmm_jsup.csv")

# either Roles or Seniority would work here:
mod <- lmer(wp ~ employment_length + seniority + (1 + seniority | dept), df)

# doesn't converge:
mod <- lmer(wp ~ employment_length + role + (1 + role | dept), df)
mod <- lmer(wp ~ employment_length + role + (1 | dept), df)

The “Wellbeing in Work” dataset contains information on employee wellbeing, assessed at baseline (start of study), 12 months post, 24 months post, and 36 months post. over the course of 36 months. Participants were randomly assigned to one of three employment conditions:

  • control: No change to employment. Employees continue at 5 days a week, with standard allocated annual leave quota.
  • unlimited_leave : Employees were given no limit to their annual leave, but were still expected to meet required targets as specified in their job description.
  • fourday_week: Employees worked a 4 day week for no decrease in pay, and were still expected to meet required targets as specified in their job description.

The researchers have two main questions: Overall, did the participants’ wellbeing stay the same or did it change? Did the employment condition groups differ in the how wellbeing changed over the assessment period?

Data are available (in .rda format) at https://uoepsy.github.io/data/wellbeingwork3.rda

variable description
ID Participant ID
TimePoint Timepoint (0 = baseline, 1 = 12 months, 2 = 24 months, 3 = 36 months)
Condition Employment Condition ('control' = 5 day week, 28 days of leave. 'unlimited_leave' = 5 days a week, unlimited leave. 'fourday_week' = 4 day week, 28 days of leave)
Wellbeing Wellbeing score (Warwick Edinburgh Mental Wellbeing Scale). Range 15 - 75, with higher scores indicating better mental wellbeing 
load(url("https://uoepsy.github.io/data/wellbeingwork3.rda"))

mod1 <- lmer(Wellbeing~TimePoint+(1+TimePoint|ID), 
             data = wellbeingwork3)
mod2 <- lmer(Wellbeing~TimePoint+Condition+(1+TimePoint|ID), 
             data = wellbeingwork3)
mod3 <- lmer(Wellbeing~TimePoint*Condition+(1+TimePoint|ID), 
             data = wellbeingwork3)
anova(mod1,mod2,mod3)

summary(mod3)

This example builds on one from the USMR course, where the lectures explored linear regression with a “toy dataset” looking at how hours of practice influences the reading age of different toy characters (see USMR Week 7 Lecture). Here, we broaden our scope to the investigation of how practice affects reading age for all toys (not just Martin’s Playmobil characters).

Data are available at https://uoepsy.github.io/data/toy2.csv containing information on 129 different toy characters that come from a selection of different families/types of toy.

variable description
toy_type Type of Toy
year Year Released
toy Character
hrs_week Hours of practice per week
R_AGE Reading Age 
df <- read_csv("https://uoepsy.github.io/data/toy2.csv")

mod <- lmer(R_AGE ~ 1 + hrs_week + (1 + hrs_week | toy_type), df)

Researchers want to study the relationship between time spent outdoors and mental wellbeing, across all of Scotland. They contact all the Local Authority Areas (LAAs) and ask them to collect data for them, with participants completing the Warwick-Edinburgh Mental Wellbeing Scale (WEMWBS), a self-report measure of mental health and well-being, and being asked to estimate the average number of hours they spend outdoors each week. Twenty of the Local Authority Areas provided data.

Data are available at https://uoepsy.github.io/data/LAAwellbeing.csv

variable description
ppt Participant Identifier
name Participant Name
laa Local Authority Area
outdoor_time Number of hours spent outdoors per week
wellbeing Wellbeing score (Warwick Edinburgh Mental Wellbeing Scale). Range 15 - 75, with higher scores indicating better mental wellbeing
density Population density of local authority area (number of people per square km) 
df <- read_csv("https://uoepsy.github.io/data/LAAwellbeing.csv")

mod1 <- lmer(wellbeing ~ density + outdoor_time + 
       (1 + outdoor_time | laa), 
       data = df) 

summary(mod1)

easter egg: check for influential people!

These data are simulated to represent data from 50 participants, each measured at 3 different time-points (pre, during, and post) on a measure of stress. Participants were randomly allocated such that half received some cognitive behavioural therapy (CBT) treatment, and half did not. This study is interested in assessing whether the two groups (control vs treatment) differ in changes in stress across the 3 time points.

The data are available at https://uoepsy.github.io/data/stressint.csv.

variable description
ppt Participant Identifier
stress Stress (range 0 to 100)
time Time (pre/post/during)
group Whether participant is in the CBT group or control group 
df <- read_csv("https://uoepsy.github.io/data/stressint.csv")
df$time <- factor(df$time, levels=c("Pre","During","Post"))

Temptation is to fit the below, but it won’t work, because each pid has only 1 obs for each time-point, so we’re overfitting (the whole Error: number of observations (=150) <= number of random effects (=150) for term message).

mod1 <- lmer(stress ~ time*group + 
               (1 + time|ppt), 
             data = df)
mod1 <- lmer(stress ~ time*group + 
               (1 |ppt), 
             data = df)

summary(mod1)

These data are simulated to represent data from a fake experiment, in which participants were asked to drive around a route in a 30mph zone. Each participant completed the route 3 times (i.e. “repeated measures”), but each time they were listening to different audio (either speech, classical music or rap music). Their average speed across the route was recorded. This is a fairly simple design, that we might use to ask “how is the type of audio being listened to associated with driving speeds?”

The data are available at https://uoepsy.github.io/data/drivingmusicwithin.csv.

variable description
pid Participant Identifier
speed Avg Speed Driven on Route (mph)
music Music listened to while driving (classical music / rap music / spoken word) 
df <- read_csv("https://uoepsy.github.io/data/drivingmusicwithin.csv")

Temptation is to fit the below, but it won’t work, because each pid has only 1 obs for each music, so we’re overfitting

mod1 <- lmer(speed ~ music + 
               (1 + music | pid), 
             data = df)
mod1 <- lmer(speed ~ music + 
               (1 | pid), 
             data = df)

summary(mod1)

Does clothing seem more attractive to shoppers when it is viewed on a model, and is this dependent on item price? 30 participants were presented with a set of pictures of items of clothing, and rated each item how likely they were to buy it. Each participant saw 20 items, ranging in price from £5 to £100. 15 participants saw these items worn by a model, while the other 15 saw the items against a white background.

Data are available at https://uoepsy.github.io/data/dapr3_mannequin.csv

variable description
purch_rating Purchase Rating (sliding scale 0 to 100, with higher ratings indicating greater perceived likelihood of purchase)
price Price presented with item (range £5 to £100)
ppt Participant Identifier
condition Whether items are seen on a model or on a white background 
df <- read_csv("https://uoepsy.github.io/data/dapr3_mannequin.csv")

#scale price to help convergence
#change 1 in price is now change of £10
df$price <- df$price/10

mod1 <- lmer(purch_rating ~ price*condition + 
       (1+price|ppt), 
       data = df)
  
summary(mod1)
Linear mixed model fit by REML ['lmerMod']
Formula: purch_rating ~ price * condition + (1 + price | ppt)
   Data: df

REML criterion at convergence: 4754.6

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.7237 -0.6389  0.0491  0.6836  3.2354 

Random effects:
 Groups   Name        Variance Std.Dev. Corr 
 ppt      (Intercept)  59.3610  7.7046       
          price         0.7131  0.8444  -0.78
 Residual             148.0384 12.1671       
Number of obs: 600, groups:  ppt, 30

Fixed effects:
                     Estimate Std. Error t value
(Intercept)           41.2807     2.4672  16.732
price                  2.4767     0.3270   7.575
conditionmodel        -1.8533     3.4891  -0.531
price:conditionmodel   1.1600     0.4624   2.509

Correlation of Fixed Effects:
            (Intr) price  cndtnm
price       -0.804              
conditinmdl -0.707  0.568       
prc:cndtnmd  0.568 -0.707 -0.804

Are children with more day-to-day routine better at regulating their emotions? A study of 200 children from 20 schools (9 private schools and 11 state schools) completed a survey containing the Emotion Dysregulation Scale (EDS) and the Child Routines Questionnaire (CRQ).

Data are available at https://uoepsy.github.io/data/crqeds.csv

variable description
schoolid School Identifier
EDS Emotion Dysregulation Score (range 1-6, higher values indicate more *dys*regulation of emotions)
CRQ Childhood Routine Questionnaire Score (range 0-7, higher values indicate more day-to-day routine)
schooltype School type (private / state) 
df <- read_csv("https://uoepsy.github.io/data/crqeds.csv")

mod1 <- lmer(EDS ~ schooltype + CRQ + 
       (1 + CRQ | schoolid), 
       data = df)

summary(mod1)

This data is from a simulated study that aims to investigate the following research question:

How do different types of audio interfere with executive functioning, and does this interference differ depending upon whether or not noise-cancelling headphones are used?

30 healthy volunteers each completed the Symbol Digit Modalities Test (SDMT) - a commonly used test to assess processing speed and motor speed - a total of 15 times. During the tests, participants listened to either no audio (5 tests), white noise (5 tests) or classical music (5 tests). Half the participants listened via active-noise-cancelling headphones, and the other half listened via speakers in the room. Unfortunately, lots of the tests were not administered correctly, and so not every participant has the full 15 trials worth of data.

Data are available at https://uoepsy.github.io/data/lmm_ef_sdmt.csv.

variable description
PID Participant ID
audio Audio heard during the test ('no_audio', 'white_noise','music')
headphones Whether the participant listened via speakers (S) in the room or via noise cancelling headphones (H)
SDMT Symbol Digit Modalities Test (SDMT) score 
df <- read_csv("https://uoepsy.github.io/data/lmm_ef_sdmt.csv")

mod1 <- lmer(SDMT ~ audio * headphones + 
               (1 + audio | PID), 
             data = df)

summary(mod1)

Let’s suppose we are studying employee job satisfaction at the university, and we want to estimate the association between pay-scale and job satisfaction, controlling for the NSS rating of departments.
We have 399 employees from 25 different departments, and we got them to fill in a job satisfaction questionnaire, and got information on what their payscale was. We have also taken information from the national student survey on the level of student satisfaction for each department.

Each datapoint here represents an individual employee, and these employees are grouped into departments.

Data are available at https://uoepsy.github.io/data/msmr_nssjobsat.csv.

variable description
NSSrating National Student Satisfaction Rating for the Department
dept Department name
payscale Pay scale of employee
jobsat Job satisfaction of employee
jobsat_binary Binary question of whether the employee considered themselves to be satisfied with their work (1) or not (0) 
df<-read_csv("https://uoepsy.github.io/data/msmr_nssjobsat.csv")

mod <- lmer(jobsat ~ 1 + NSSrating + payscale + (1 + payscale | dept), df)

We have data from a large sample of great apes who have been studied between the ages of 1 to 10 years old (i.e. during adolescence). Our data includes 4 species of great apes: Chimpanzees, Bonobos, Gorillas and Orangutans. Each ape has been assessed on a primate dominance scale at various ages. Data collection was not very rigorous, so apes do not have consistent assessment schedules (i.e., one may have been assessed at ages 1, 3 and 6, whereas another at ages 2 and 8).

The researchers are interested in examining how the adolescent development of dominance in great apes differs between species.

Data on the dominance scores of the apes are available at https://uoepsy.github.io/data/lmm_apeage.csv and the information about which species each ape is are in https://uoepsy.github.io/data/lmm_apespecies.csv.

Table 1: Data Dictionary: lmm_apespecies.csv
variable description
ape Ape Name
species Species (Bonobo, Chimpanzee, Gorilla, Orangutan)
Table 2: Data Dictionary: lmm_apeage.csv
variable description
ape Ape Name
age Age at assessment (years)
dominance Dominance (Z-scored) 
dfape1 <- read_csv("https://uoepsy.github.io/data/lmm_apespecies.csv")
dfape2 <- read_csv("https://uoepsy.github.io/data/lmm_apeage.csv")

df <- full_join(dfape1, dfape2)

some cleaning is needed:

df <- df |> 
  mutate(
    # fix species typos
    species = case_when(
      species %in% c("chimp","chimpanzee") ~ "chimp",
      species %in% c("gorilla","gorrila") ~ "gorilla",
      TRUE ~ species
    )
  ) |>
    filter(
      # get rid of ages -99
      age > 0, 
      # keep when dominance is between -5 and 5 
      # (5 here is a slightly arbitrary choice, but you can see from
      # our checks that this will only exclude the two extreme datapoints
      # that are 21.2 and 19.4
      (dominance < 5 & dominance > -5) 
    )

model comparison answers “do species differ in growth of dominance?”
for “how do specific species differ?” we look at fixed effects.

mod <- lmer(dominance ~ age * species + (1 + age | ape), df)
mod.rstr <- lmer(dominance ~ age + species + (1 + age | ape), df)

anova(mod.rstr, mod)

A study is interested in examining whether engaging in mindfulness can prevent cognitive decline in older adults. They recruit a sample of 20 participants at age 60, and administer the Addenbrooke’s Cognitive Examination (ACE) every 2 years (until participants were aged 78). Half of the participants complete weekly mindfulness sessions, while the remaining participants did not.

Data are available at https://uoepsy.github.io/data/lmm_mindfuldecline.csv.

variable description
sitename Site Identifier
ppt Participant Identifier
condition Whether the participant engages in mindfulness or not (control/mindfulness)
visit Study Visit Number (1 - 10)
age Age (in years) at study visit
ACE Addenbrooke's Cognitive Examination Score. Scores can range from 0 to 100
imp Clinical diagnosis of cognitive impairment ('imp' = impaired, 'unimp' = unimpaired) 
df <- read_csv("https://uoepsy.github.io/data/lmm_mindfuldecline.csv")

if we don’t recenter age, then the intercept variability (1|ppt) is estimated way back 60 years before we collected any data. The slopes will basically perfectly predicted these intercept differences, so the model will be singular.
re-centering will help.

#recenter age
df$ageC <- df$age-60

mod1 <- lmer(ACE ~ 1 + ageC * condition + 
               (1 + ageC | ppt), 
             data = df)

summary(mod1)

A large study involving 14 different research centers is interested in examining whether engaging in mindfulness can prevent cognitive decline in older adults. Each site recruits between 15 and 30 participants at age 60, and administer the Addenbrooke’s Cognitive Examination (ACE) every 2 years (until participants were aged 78). For each center, roughly half of the participants engaged with daily mindfulness sessions, while the remaining participants did not.

Data are available at https://uoepsy.github.io/data/lmm_mindfuldeclineFULL.csv

variable description
sitename Site Identifier
ppt Participant Identifier
condition Whether the participant engages in mindfulness or not (control/mindfulness)
visit Visit number (1 - 10)
age Age (years) at visit
ACE Addenbrooke's Cognitive Examination Score. Scores can range from 0 to 100
imp Clinical diagnosis of cognitive impairment ('imp' = impaired, 'unimp' = unimpaired)

as above but it’s nested

df <- read_csv("https://uoepsy.github.io/data/lmm_mindfuldeclineFULL.csv")
df$ageC <- df$age-60

# maximal model won't converge
mmod <- lmer(ACE ~ 1 + ageC * condition + 
              ( 1 + ageC * condition | sitename) +
               (1 + ageC | sitename:ppt), 
             data = df)

# probably simplify to 
mod <- lmer(ACE ~ 1 + ageC * condition + 
              ( 1 + ageC | sitename) +
               (1 + ageC | sitename:ppt), 
             data = df)

summary(mod1)

Suppose that we conducted an experiment on a sample of 20 staff members from the Psychology department to investigate effects of CBD consumption on stress over the course of the working week. Participants were randomly allocated to one of two conditions: the control group continued as normal, and the CBD group were given one CBD drink every day. Over the course of the working week (5 days) participants stress levels were measured using a self-report questionnaire.

Data are available at https://uoepsy.github.io/data/stressweek1.csv.

variable description
dept Department
pid Participant Name
CBD Whether or not they were allocated to the control group (N) or the CBD group (Y)
measure Measure used to assess stress levels
day Day of the working week (1 to 5)
stress Stress Level (standardised) 
df <- read_csv("https://uoepsy.github.io/data/stressweek1.csv")
# re-center 'day' so the intercept is day 1
df$day <- df$day-1 

mod1 <- lmer(stress ~ 1 + day * CBD + 
               (1 + day | pid), 
             data = df)

summary(mod1)

As for Version 1 of this study (see above), but instead of a sample of 20 participants from the psychology staff, we have 240 people from various departments such as History, Philosophy, Art, etc..

Data are available at https://uoepsy.github.io/data/stressweek_nested.csv.

variable description
dept Department
pid Participant Name
CBD Whether or not they were allocated to the control group (N) or the CBD group (Y)
measure Measure used to assess stress levels
day Day of the working week (1 to 5)
stress Stress Level (standardised) 
df <- read_csv("https://uoepsy.github.io/data/stressweek_nested.csv")

# re-center 'day' so the intercept is day 1
df$day <- df$day-1 

# removed day*CBD|dept to obtain convergence
mod1 <- lmer(stress ~ 1 + day * CBD + 
               (1 + day + CBD | dept) +
               (1 + day | dept:pid), 
             data = df)

summary(mod1)

As for Version 1 of this study (see above), with 20 staff members from the Psychology department, but instead of taking a measurement only on a self-report scale, we took 10 different measures every time point (cortisol levels, blood pressure, heart rate variability, various questionnaires etc).

Data are available at https://uoepsy.github.io/data/stressweek_crossed.csv

variable description
dept Department
pid Participant Name
CBD Whether or not they were allocated to the control group (N) or the CBD group (Y)
measure Measure used to assess stress levels
day Day of the working week (1 to 5)
stress Stress Level (standardised) 
df <- read_csv("https://uoepsy.github.io/data/stressweek_crossed.csv")

# re-center 'day' so the intercept is day 1
df$day <- df$day-1 

# removed day*CBD|dept to obtain convergence
mod1 <- lmer(stress ~ 1 + day * CBD + 
                (1 + day + CBD | measure) +
                (1 + day | pid), 
             data = df)

summary(mod1)

These data are simulated to represent a large scale international study of cognitive aging, for which data from 17 research centers has been combined. The study team are interested in whether different cognitive domains have different trajectories as people age. Do all cognitive domains decline at the same rate? Do some decline more steeply, and some less? The literature suggests that scores on cognitive ability are predicted by educational attainment, so they would like to control for this.

Each of the 17 research centers recruited a minimum of 14 participants (Median = 21, Range 14-29) at age 48, and recorded their level of education (in years). Participants were then tested on 5 cognitive domains: processing speed, spatial visualisation, memory, reasoning, and vocabulary. Participants were contacted for follow-up on a further 9 occasions (resulting in 10 datapoints for each participant), and at every follow-up they were tested on the same 5 cognitive domains. Follow-ups were on average 3 years apart (Mean = 3, SD = 0.8).

Data are available at https://uoepsy.github.io/data/cogdecline.csv.

variable description
cID Center ID
pptID Participant Identifier
educ Educational attainment (years of education)
age Age at visit (years)
processing_speed Score on Processing Speed domain task
spatial_visualisation Score on Spatial Visualisation domain task
memory Score on Memory domain task
reasoning Score on Reasoning domain task
vocabulary Score on Vocabulary domain task

we need to reshape this data! we don’t have a single variable “score” here, because it’s actually split across 5 columns (one for each domain). So we reshape those columns to have a variable called “score” and a variable indicating which domain it is a score of (we’ll call it “domain”):

df <- read_csv("https://uoepsy.github.io/data/cogdecline.csv")

# reshape
df <- df |> pivot_longer(processing_speed:vocabulary,
                   names_to = "domain",
                   values_to = "score")

# recenter age and educ
df$age <- (df$age - 48)/5
df$educ <- df$educ - min(df$educ)

this won’t converge:

mod1 <- lmer(score ~ educ + age * domain + 
               (1 + educ + age * domain | cID) + 
               (1 + age * domain | cID:pptID),
             data = df)

this will - it’s using the trick of putting the domain on the RHS here, to still have different slopes of score~age for each domain:

mod1 <- lmer(score ~ educ + age * domain + 
               (1 | cID) + 
               (1 + age | cID:pptID) +
               (1 + age | cID:pptID:domain),
             data = df,
             control=lmerControl(optimizer="bobyqa"))

summary(mod1)

This is synthetic data from a randomised controlled trial to evaluate the efficacy of a psychoeducational treatment on anxiety disorders, in which 30 therapists randomly assigned patients (each therapist saw between 2 and 28 patients) to a control or treatment group, and monitored their scores over time on a measure of generalised anxiety disorder (GAD7 - a 7 item questionnaire with 5 point likert scales).

The control group of patients received standard sessions offered by the therapists. For the treatment group, 10 mins of each sessions was replaced with a specific psychoeducational component, and patients were given relevant tasks to complete between each session. All patients had monthly therapy sessions. Generalised Anxiety Disorder was assessed at baseline and then every visit over 4 months of sessions (5 assessments in total).

Data are available at https://uoepsy.github.io/data/lmm_gadeduc.csv

You can find a data dictionary below:

variable description
patient A patient code in which the labels take the form <Therapist initials>_<group>_<patient number>.
visit_0 Score on the GAD7 at baseline
visit_1 GAD7 at 1 month assessment
visit_2 GAD7 at 2 month assessment
visit_3 GAD7 at 3 month assessment
visit_4 GAD7 at 4 month assessment

this one needs lots of reshaping and sorting out first, but it can actually be done with minimal code using things like separate()

df <- read_csv("https://uoepsy.github.io/data/lmm_gadeduc.csv")
df <- df |> 
  pivot_longer(2:last_col(), names_to="visit",values_to="GAD") |>
  mutate(
    visit = as.numeric(gsub("visit_","",visit))
  ) |>
  separate(patient, into=c("therapist","group","patient"), sep="_")

mod <- lmer(GAD~ visit*group+ 
              (1+visit*group|therapist)+
              (1+visit|therapist:patient),
            df)

In 2010 A US state’s commissioner for education was faced with growing community concern about rising levels of adolescent antisocial behaviours.

After a series of focus groups, the commissioner approved the trialing of an intervention in which yearly Parent Management Training (PMT) group sessions were offered to the parents of a cohort of students entering 10 different high schools. Every year, the parents were asked to fill out an informant-based version of the Aggressive Behaviour Scale (ABS), measuring verbal and physical abuse, socially inappropriate behavior, and resisting care. Where possible, the same parents were followed up throughout the child’s progression through high school. Alongside this, parents from a cohort of students entering 10 further high schools in the state were recruited to also complete the same informant-based ABS, but were not offered the PMT group sessions.
The commissioner has two main questions: Does the presentation of aggressive behaviours increase as children enter the secondary school system? Is there any evidence for the effectiveness of Parent Management Training (PMT) group sessions in curbing the rise of aggressive behaviors during a child’s transition into the secondary school system?

Data are available at https://uoepsy.github.io/data/abs_intervention.csv

variable description
schoolid School Name
ppt Participant Identifier
age Age (years)
interv Whether or not parents attended Parent Management Training (PMT) group sessions (0 = No, 1 = Yes)
ABS Aggressive Behaviours Scale. Measures verbal and physical abuse, socially inappropriate behavior, and resisting care. Scores range from 0 to 100, with higher scores indicating more aggressive behaviours.

Check here: https://uoepsy.github.io/dapr3/2425/lectures/05recap.html#/the-research-process-model-specification

These data are simulated to imitate an experiment that investigates the effect of visual non-verbal communication (i.e. gestures, facial expressions) on joke appreciation. 90 Participants took part in the experiment, in which they each rated how funny they found a set of 30 jokes. For each participant, the order of these 30 jokes was randomly set for each run of the experiment. For each participant, the set of jokes was randomly split into two halves, with the first half being presented in audio-only, and the second half being presented in audio and video. This meant that each participant saw 15 jokes with video and 15 without, and each joke would be presented in with video roughly half of the times it was seen.

The researchers want to investigate whether the delivery (audio/audiovideo) of jokes is associated with differences in humour-ratings.

Data are available at https://uoepsy.github.io/data/lmm_laughs.csv

Table 3: Data Dictionary: lmm_laughs.csv
variable description
ppt Participant Identification Number
joke_label Joke presented
joke_id Joke Identification Number
delivery Experimental manipulation: whether joke was presented in audio-only ('audio') or in audiovideo ('video')
rating Humour rating chosen on a slider from 0 to 100 
df <- read_csv("https://uoepsy.github.io/data/lmm_laughs.csv")

mod <- lmer(rating ~ delivery + 
              (1 + delivery | joke_id) +
              (1 + delivery | ppt),
            data = df)

worth looking at random effects for different jokes to see which ones are funniest etc.
The jokes are all from some study 10 years ago that aimed to find “the worlds funniest joke”

These data are from an experiment designed to investigate how the realism of video games is associated with more/less unnecessarily aggressive gameplay, and whether this differs depending upon a) the playing mode (playing on a screen vs VR headset), and b) individual differences in the ‘dark triad’ personality traits.

The experiment involved playing 10 levels of a game in which the objective was to escape a maze. Various obstacles and other characters were present throughout the maze, and players could interact with these by side-stepping or jumping over them, or by pushing or shooting at them. All of these actions took the same amount of effort to complete (pressing a button), and each one achieved the same end (moving beyond the obstacle and being able to continue through the maze).

Each participant completed all 10 levels twice, once in which all characters were presented as cartoons, and once in which all characters were presented as realistic humans and animals. The layout of the level was identical in both, the only difference being the depiction of objects and characters. For each participant, these 20 levels (\(2 \times 10\) mazes) were presented in a random order. Half of the participants played via a screen, and the other half played via a VR headset. For each level played, we have a record of “needless game violence” (NGV) which was calculated via the number of aggressive (pushing/shooting) actions taken (+0.5 for every action that missed an object, +1 for every action aimed at an inanimate object, and +2 for every action aimed at an animate character).
Prior to the experiment, each participant completed the Short Dark Triad 3 (SD-3), which measures the three traits of machiavellianism, narcissism, and psychopathy.

Data are available at https://uoepsy.github.io/data/NGV.csv

variable description
PID Participant number
age Participant age (years)
level Maze level (1 to 20)
character Whether the objects and characters in the level were presented as 'cartoon' or as 'realistic'
mode Whether the participant played via a screen or with a VR headset
P Psycopathy Trait from SD-3 (score 1-5)
N Narcissism Trait from SD-3 (score 1-5)
M Machiavellianism Trait from SD-3 (score 1-5)
NGV Needless Game Violence metric

(you could also try to fit the interactions in the random effects here but i’m not going to even try!)

m0 = lmer(NGV ~ character * (mode + P + M + N) + 
            (1 + character | PID) + 
            (1 + character + mode + P + M + N | level), data = ngv)

after some simplification, I end up at the model below. You might end up at a slightly different random effect structure, and that is completely okay! The important thing is to be transparent in your decisions.

m1 = lmer(NGV ~ character * (mode + P + M + N) + 
            (1 + character | PID) + 
            (1 + mode | level), data = ngv)

These data are simulated to represent data from 30 participants who took part in an experiment designed to investigate whether fluency of speech influences how believable an utterance is perceived to be.

Each participant listened to the same 20 statements, with 10 being presented in fluent speech, and 10 being presented with a disfluency (an “erm, …”). Fluency of the statements was counterbalanced such that 15 participants heard statements 1 to 10 as fluent and 11 to 20 as disfluent, and the remaining 15 participants heard statements 1 to 10 as disfluent, and 11 to 20 as fluent. The order of the statements presented to each participant was random. Participants rated each statement on how believable it is on a scale of 0 to 100.

Data are available at https://uoepsy.github.io/data/erm_belief.csv.

variable description
ppt Participant Identifier
trial_n Trial number
sentence Statement identifier
condition Condition (fluent v disfluent)
belief belief rating (0-100)
statement Statement 
df <- read_csv("https://uoepsy.github.io/data/erm_belief.csv")
# make trial_n numeric
df$trial_n <- as.numeric(gsub("trial_","",df$trial_n))
# relevel condition:
df$condition <- factor(df$condition, levels=c("fluent","disfluent"))

# having (trial_n | ppt) doesn't converge, so simplify to:
mod1 <- lmer(belief ~ trial_n + condition + 
               (1 | ppt) + 
               (1 + condition | statement), 
             data = df)

summary(mod1)

easter egg: plot your ranefs

dotplot.ranef.mer(ranef(mod1))$statement

A research study is investigating how anxiety is associated with drinking habits. Data was collected from 50 participants from 5 centers. Researchers administered the generalised anxiety disorder (GAD-7) questionnaire to measure levels of anxiety over the past week, and collected information on the units of alcohol participants had consumed within the week. Each participant was observed on 10 different occasions.

The researchers are also interested in testing an intervention (given to half of the participants) - they want to know if this changes the association between anxiety and alcohol consumption.

variable description
alcunits Number of units of alcohol consumed over the past week
gad Score on the Generalised Anxiety Disorder scale (scores 0-3 on 7 questions are totalled for an overall score)
intervention Whether the participant is part of the intervention group (1) or not (0)
center Center ID
ppt Participant ID

We actually have participants nested in center here, but there are only 5 centers..

df <- read_csv("https://uoepsy.github.io/data/lmm_alcgad.csv")

first though, we’ll calculate ppt means and ppt deviations-from-means

df <- df |> 
  group_by(ppt) |>
  mutate(
    gadm = mean(gad),
    gaddev = gad - mean(gad)
  ) |> ungroup()

this works, but bear in mind we do only have 5 centers..

mod <- lmer(alcunits ~ gadm + gaddev + 
       (1 + gaddev | center) +
       (1 + gaddev | center:ppt),
     df)

this would be defensible too:

mod <- lmer(alcunits ~ center + gadm + gaddev + 
       (1 + gaddev | ppt),
     df)

We also have the intervention question, which to meet convergence might need to do something like:

mod <- lmer(alcunits ~ center + (gadm + gaddev)*intervention + 
       (1 | ppt),
     df)

A researcher is interested in the efficacy of physiotherapy in helping people to regain normal physical functioning. They are curious whether doing more physiotherapy leads to better outcomes, or if it is possibly that the patients who tend to do more of their exercises tend to have better outcomes. 20 in-patients from 2 different hospitals (1 private, 1 govt funded) were monitored over the course of their recovery following knee-surgery. Every day, the time each patient spent doing their physiotherapy exercises was recorded. At the end of each day, participants completed the “Time get up and go” task, a measure of physical functioning.

Data are available at https://uoepsy.github.io/data/dapr3_tgu.csv

variable description
tgu Time Get up and Go Task - measure of physical functioning. Scored in minutes, with lower scores indicating better physical functioning
phys Minutes of physiotherapy exercises completed that day
hospital Hospital ID
patient Patient ID
prioritylevel Priority level of patients' surgery (rank 1-4, with 1 being most urgent surgey, and 4 being least urgent)
private 0 = government funded hospital, 1 = private hospital

patients are nested in hospitals, but there are only 2 hospitals!
just shove it in as fixed predictor

df <- read_csv("https://uoepsy.github.io/data/dapr3_tgu.csv")

df <- df |> group_by(patient) |>
  mutate(
    physm = mean(phys),
    physdev = phys - mean(phys)
  ) |> ungroup()

mod <- lmer(tgu ~ hospital + physm + physdev + 
              (1 + physdev | patient),
            data = df)

These data are simulated based on the “Big-fish-little-pond” effect in educational literature.

We are interested in better understanding the relationship between school children’s grades and their academic self-concept (their self-perception of ability in specific and general academic disciplines).

We have data from 20 classes of children, capturing information on their grades at school (range 0 to 10), and a measure of academic self-concept:

Data are available at https://uoepsy.github.io/data/lmm_bflpe.csv

variable description
grade Children's School Grade
class Class Identifier
self_concept Children's Self-Concept Score
child Child Identifier 
df <- read_csv("https://uoepsy.github.io/data/lmm_bflpe.csv")

df <- df |> group_by(class) |>
  mutate(
    gradem = mean(grade),
    gradedev = grade - mean(grade)
  )

mod <- lmer(self_concept ~ gradem + gradedev + 
              (1 + gradedev | class), 
            data = df)

This study is interested in evaluating whether peoples’ hunger levels are associated with their levels of irritability (i.e., “the hangry hypothesis”), and if this differs between people on a diet vs those who aren’t. 81 participants were recruited into the study. Once a week for 5 consecutive weeks, participants were asked to complete two questionnaires, one assessing their level of hunger, and one assessing their level of irritability. The time and day at which participants were assessed was at a randomly chosen hour between 7am and 7pm each week. 46 of the participants were following a five-two diet (five days of normal eating, 2 days of fasting), and the remaining 35 were following no specific diet.

Data are available at https://uoepsy.github.io/data/hangry.csv

variable description
q_irritability Score on irritability questionnaire (0:100)
q_hunger Score on hunger questionnaire (0:100)
ppt Participant Identifier
fivetwo Whether the participant follows the five-two diet 
df <- read_csv("https://uoepsy.github.io/data/hangry.csv")

df <- df |> group_by(ppt) |>
  mutate(
    hungerm = mean(q_hunger),
    hungerdev = q_hunger - mean(q_hunger)
  )

mod <- lmer(q_irritability ~ (hungerm + hungerdev) * fivetwo +
              (1 + hungerdev | ppt), 
            data = df,
            control=lmerControl(optimizer="bobyqa"))

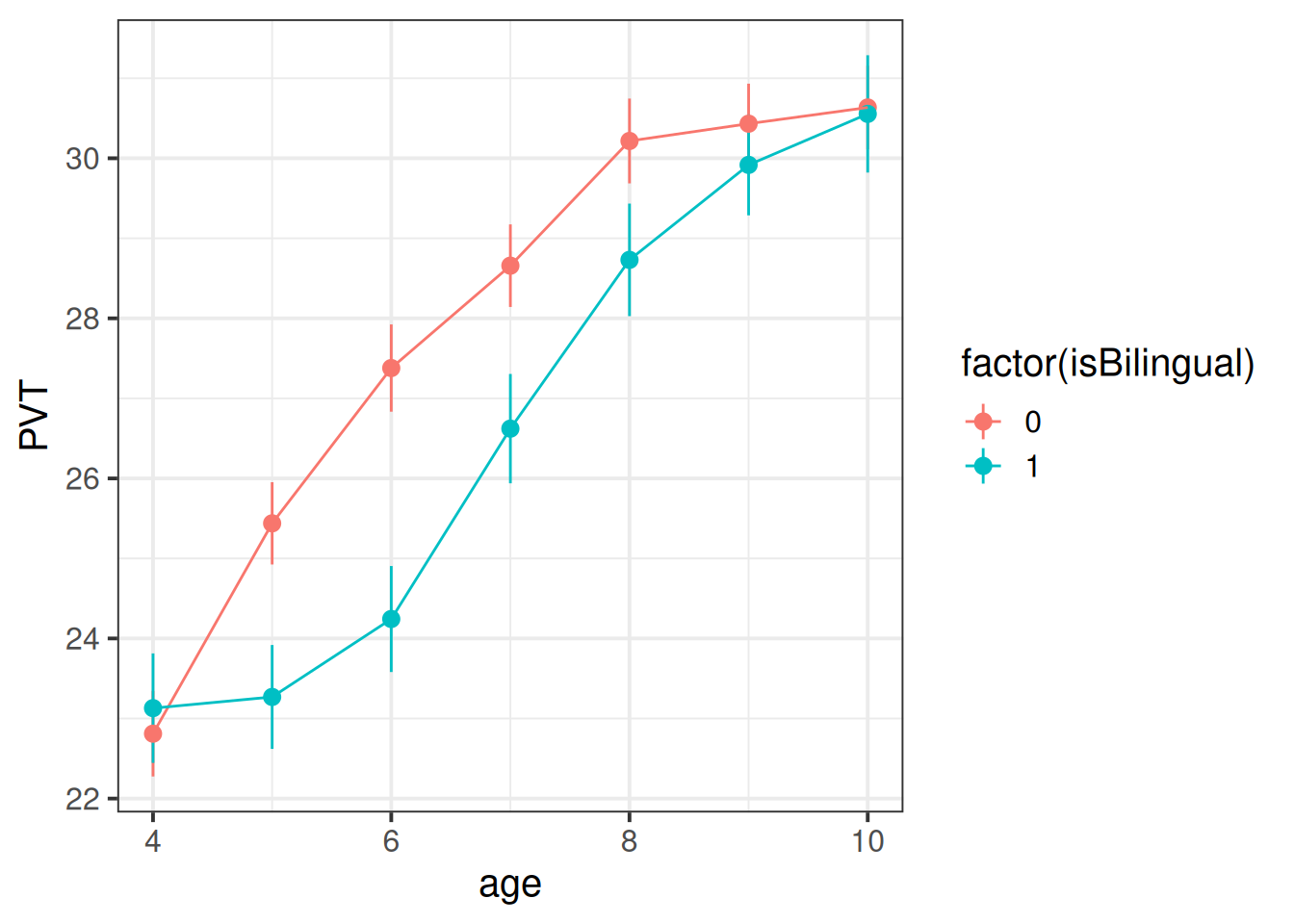
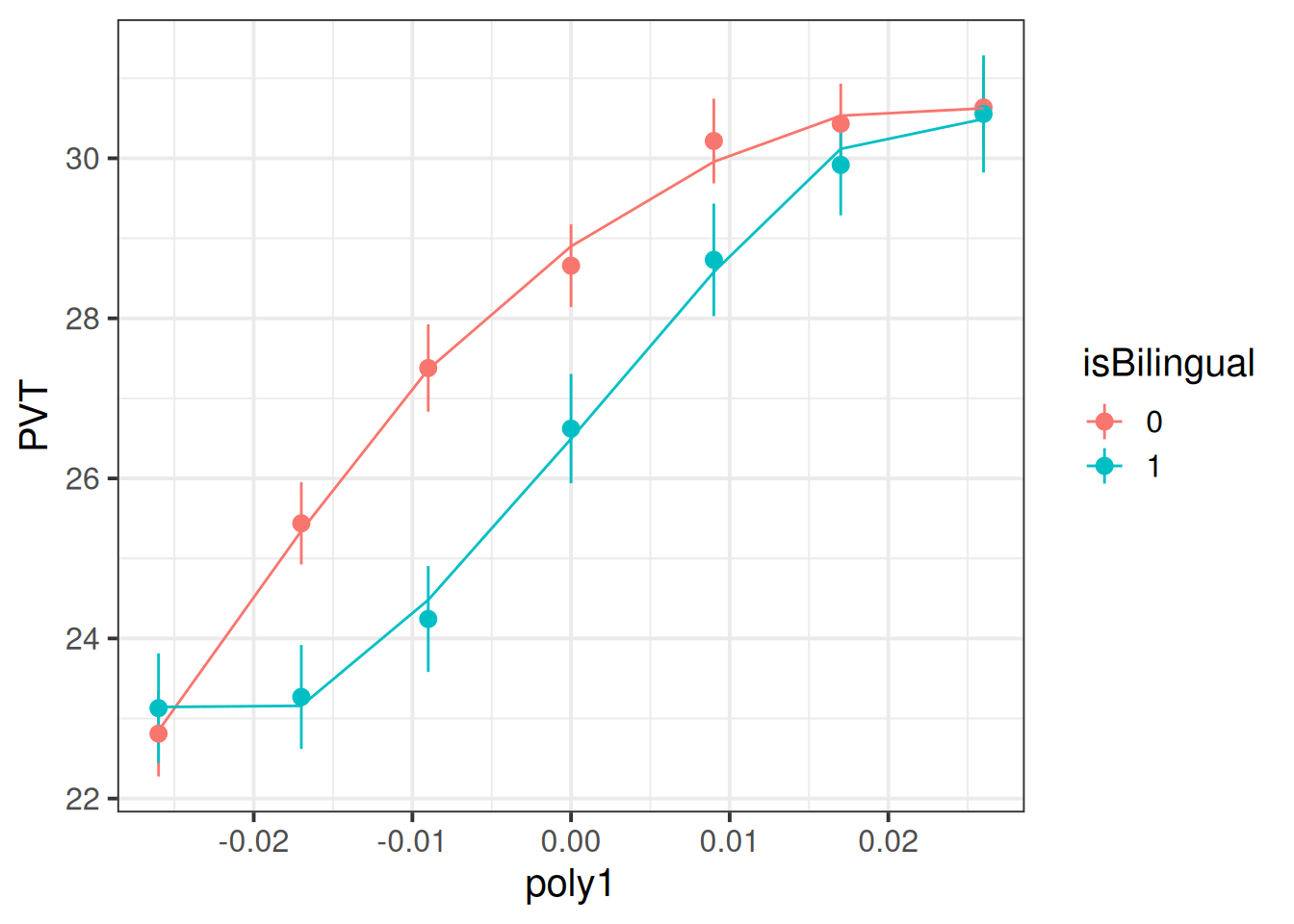
488 children from 30 schools were included in the study. Children were assessed on a yearly basis for 7 years throughout primary school on a measure of vocabulary administered in English, the Picture Vocab Test (PVT). 295 were monolingual English speakers, and 193 were bilingual (english + another language).

Previous research conducted on monolingual children has suggested that that scores on the PVT increase steadily up until the age of approximately 7 or 8 at which point they begin to plateau. The aim of the present study is to investigate differences in the development of vocabulary between monolingual and bilingual children.

Data are available at https://uoepsy.github.io/data/pvt_bilingual.csv.

variable description
child Child's name
school School Identifier
isBilingual Binary variable indicating whether the child is monolingual (0) or bilingual (1)
age Age (years)
PVT Score on the Picture Vocab Test (PVT). Scores range 0 to 60

Let’s read in the data:

pvt <- read_csv("https://uoepsy.github.io/data/pvt_bilingual.csv")

We have 30 distinct schools:

n_distinct(pvt$school)
[1] 30

And 418 distinct children. Is that right?

n_distinct(pvt$child)
[1] 418

Given that the pvt$child variable is just the first name of the child, it’s entirely likely that there will be, for instance more than one “Martin”.

This says that there are 487!

pvt |> count(school, child) |> nrow()
[1] 487

But wait… we could still have issues. What if there were 2 “Martin”s at the same school??

pvt |> 
  # count the school-children groups
  count(school, child) |> 
  # arrange the output so that the highest 
  # values of the 'n' column are at the top
  arrange(desc(n))
# A tibble: 487 × 3
   school    child        n
   <chr>     <chr>    <int>
 1 School 14 James       14
 2 School 14 Michelle    14
 3 School 15 Michael     14
 4 School 21 Daniel      14
 5 School 3  Jackson     14
 6 School 5  Raven       14
 7 School 9  Kaamil      14
 8 School 1  Allyssa      7
 9 School 1  Armon        7
10 School 1  Dakota       7
# ℹ 477 more rows

Aha! There are 7 cases where schools have two children of the same name. Remember that each child was measured at 7 timepoints. We shouldn’t have people with 14!

If we actually look at the data, we’ll see that it is very neatly organised, with each child’s data together. This means that we could feasibly make an educated guess that, e.g., the “Jackson” from “School 3” in rows 155-161 is different from the “Jackson” from “School 3” at rows 190-196.

Because of the ordering of our data, we can do something like this:

pvt <- 
  pvt |>
  # group by the school and child
  group_by(school, child) |>
  mutate(
    # make a new variable which counts from 1 to 
    # the number of rows for each school-child
    n_obs = 1:n()
  ) |>
  # ungroup the data
  ungroup() |>
  mutate(
    # change it so that if the n_obs is >7, the 
    # child becomes "[name] 2", to indicate they're the second
    # child with that name
    child = ifelse(n_obs>7, paste0(child," 2"), child)
  )

Now we have 494!

pvt |> count(school, child) |> nrow()
[1] 494

And nobody has anything other than 7 observations!

pvt |> count(school, child) |>
  filter(n != 7)
# A tibble: 0 × 3
# ℹ 3 variables: school <chr>, child <chr>, n <int>

Phew!

Okay, let’s just fit an intercept-only model:

pvt_null <- lmer(PVT ~ 1 +  (1 | school/child), data = pvt)
summary(pvt_null)
Linear mixed model fit by REML ['lmerMod']
Formula: PVT ~ 1 + (1 | school/child)
   Data: pvt

REML criterion at convergence: 23844.1

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.7768 -0.5984  0.0068  0.5744  4.1806 

Random effects:
 Groups       Name        Variance Std.Dev.
 child:school (Intercept) 33.48    5.786   
 school       (Intercept) 19.76    4.445   
 Residual                 43.59    6.602   
Number of obs: 3458, groups:  child:school, 494; school, 30

Fixed effects:
            Estimate Std. Error t value
(Intercept)  27.5263     0.8667   31.76

As we can see from summary(bnt_null), the random intercept variances are 33.48 for child-level, 19.76 for school-level, and the residual variance is 43.59.

So child level differences account for \(\frac{33.48}{33.48 + 19.76 + 43.59} = 0.35\) of the variance in PVT scores, and child & school differences together account for \(\frac{33.48 + 19.76}{33.48 + 19.76 + 43.59} = 0.55\) of the variance.

Here’s an initial plot too:

ggplot(pvt, aes(x=age,y=PVT,col=factor(isBilingual)))+
  stat_summary(geom="pointrange")+
  stat_summary(geom="line")

I feel like either raw or orthogonal polynomials would be fine here - there’s nothing explicit from the study background about stuff “at baseline”. There’s the stuff about the plateau at 7 or 8, but we can get that from the model plots. Orthogonal will allow us to compare the trajectories overall (their linear trend, the ‘curviness’ and ‘wiggliness’).

An additional benefit of orthogonal polynomials is that we are less likely to get singular fits when we include polynomial terms in our random effects. Remember, raw polynomials are correlated, so often the by-participant variances in raw poly terms are highly correlated.

I’ve gone for 3 degrees of polynomials here because the plot above shows a bit of an S-shape for the bilinguals.

pvt <- pvt |> mutate(
  poly1 = poly(age, 3)[,1],
  poly2 = poly(age, 3)[,2],
  poly3 = poly(age, 3)[,3],
  isBilingual = factor(isBilingual)
)

These models do not converge.
I’ve tried to preserve the by-child random effects of time, because while I think Schools probably do vary, School’s all teach the same curriculum, whereas there’s a lot of varied things that can influence a child’s vocabulary, both in and out of school

mod1 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + (poly1 + poly2 + poly3)*isBilingual | school) + 
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)

mod2 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + isBilingual * (poly1 + poly2) + poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)

mod3 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + isBilingual * poly1 + poly2 + poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)

mod4 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + isBilingual + poly1 + poly2 + poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)

mod5 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + isBilingual + poly1 + poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)
# relative to the variance in time slopes, there's v little by-school variance in bilingual differences in vocab

mod6 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + poly1 + poly2 +  poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)
# looks like curvature doesn't vary between schools much as linear and wiggliness

this one does!

mod7 <- lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + poly1 + poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)
library(broom.mixed)
augment(mod7) |> 
  mutate(
    poly1 = round(poly1, 3) # because of rounding errors that make plot weird
  ) |>
  ggplot(aes(x=poly1,col=isBilingual))+
  stat_summary(geom="pointrange",aes(y=PVT))+
  stat_summary(geom="line", aes(y=.fitted))

refitted with lmerTest:

mod7 <- lmerTest::lmer(PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + 
       (1 + poly1 + poly3 | school) +
       (1 + (poly1 + poly2 + poly3) | school:child),
     data = pvt)

summary(mod7)
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: PVT ~ 1 + (poly1 + poly2 + poly3) * isBilingual + (1 + poly1 +  
    poly3 | school) + (1 + (poly1 + poly2 + poly3) | school:child)
   Data: pvt

REML criterion at convergence: 23076.6

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-4.4455 -0.5498 -0.0004  0.5261  4.4198 

Random effects:
 Groups       Name        Variance Std.Dev. Corr             
 school:child (Intercept)   34.86   5.904                    
              poly1       1843.79  42.939    0.01            
              poly2       3944.17  62.803   -0.08  0.23      
              poly3        684.39  26.161    0.19  0.61  0.87
 school       (Intercept)   19.96   4.468                    
              poly1        927.01  30.447   -0.40            
              poly3        335.86  18.327   -0.52 -0.12      
 Residual                   31.93   5.651                    
Number of obs: 3458, groups:  school:child, 494; school, 30

Fixed effects:
                    Estimate Std. Error        df t value Pr(>|t|)    
(Intercept)          27.9464     0.8986   31.1147  31.099  < 2e-16 ***
poly1               157.0377     9.5728   39.6249  16.404  < 2e-16 ***
poly2               -48.9606     8.0941  517.6683  -6.049 2.80e-09 ***
poly3                -1.2818     8.1745   61.5436  -0.157  0.87591    
isBilingual1         -1.2113     0.5863  465.7959  -2.066  0.03939 *  
poly1:isBilingual1   16.6095    12.3125  501.8217   1.349  0.17795    
poly2:isBilingual1   56.2609    12.9495  517.6683   4.345 1.68e-05 ***
poly3:isBilingual1  -34.3292    11.8629 1218.1024  -2.894  0.00387 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
            (Intr) poly1  poly2  poly3  isBln1 pl1:B1 pl2:B1
poly1       -0.215                                          
poly2       -0.013  0.026                                   
poly3       -0.184 -0.004  0.072                            
isBilingul1 -0.250 -0.001  0.020 -0.020                     
ply1:sBlng1  0.000 -0.500 -0.020 -0.022 -0.001              
ply2:sBlng1  0.008 -0.016 -0.625 -0.045 -0.033  0.033       
ply3:sBlng1 -0.009 -0.020 -0.050 -0.566  0.034  0.038  0.079
optimizer (nloptwrap) convergence code: 0 (OK)
boundary (singular) fit: see help('isSingular')
term est p interpretation
(Intercept) 27.95 * average vocab score at the mean age (for monolingual)
poly1 157.04 * vocab increases over time (for monolingual children)
poly2 -48.96 * the increase in vocab becomes more gradual (for monolingual children)
poly3 -1.28 no significant wiggliness to vocab trajectory of the average monolingual child
isBilingual1 -1.21 * average vocab score at mean age is lower for bilingual vs monolingual children
poly1:isBilingual1 16.61 no significant difference in linear trend of vocab for bilingual vs monolingual
poly2:isBilingual1 56.26 * curvature for vocab trajectory of bilingual children significantly differs from that of monolinguals
poly3:isBilingual1 -34.33 * wiggliness for vocab trajectory of bilingual children significantly differs from that of monolinguals

From the random effects, we get even more information!
School’s vary in the average child vocab score at mean age with an SD of 4.5. More school level variation in linear trends than in curvature. Schools with higher vocab scores at the mean age tend to have lower linear increase, and also a more negative curvature.
Within schools, children vary in the vocab scores at mean age with an SD of 5.9. Lots of child-level variation in curvature and linear increases, slightly less variation in wiggliness.

VarCorr(mod7)
 Groups       Name        Std.Dev. Corr                
 school:child (Intercept)  5.9043                      
              poly1       42.9394   0.005              
              poly2       62.8027  -0.078  0.227       
              poly3       26.1608   0.192  0.608  0.872
 school       (Intercept)  4.4682                      
              poly1       30.4469  -0.403              
              poly3       18.3266  -0.525 -0.117       
 Residual                  5.6511

These data are available at https://uoepsy.github.io/data/Az.rda. You can load the dataset using:

load(url("https://uoepsy.github.io/data/Az.rda"))

and you will find the Az object in your environment.

The Az object contains information on 30 Participants with probable Alzheimer’s Disease, who completed 3 tasks over 10 time points: A memory task, and two scales investigating ability to undertake complex activities of daily living (cADL) and simple activities of daily living (sADL). Performance on all of tasks was calculated as a percentage of total possible score, thereby ranging from 0 to 100.

We’re interested in whether performance on these tasks differed at the outset of the study, and if they differed in their subsequent change in performance.

variable description
Subject Unique Subject Identifier
Time Time point of the study (1 to 10)
Task Task type (Memory, cADL, sADL)
Performance Score on test (range 0 to 100) 
# TODO ANALYSIS

Previous research has evidenced a notable dip in happiness for middle-aged humans. Interestingly, this phenomenon has even been observed in other primates, such as chimpanzees.

The present study is interested in examining whether the ‘middle-age slump’ happens to a similar extent for Orangutans as it does for Chimpanzees.

200 apes (117 Chimps and 83 Orangutans) were included in the study. All apes were studied from early adulthood (10-12 years old for most great apes), and researchers administered the Happiness in Primates (HiP) scale to each participant every 3 years, up until the age of 40.

Data are available at https://uoepsy.github.io/data/midlife_ape.csv.

The dataset has already been cleaned, and the researchers have confirmed that it includes 117 Chimps and 83 Orangutans, and every ape has complete data (i.e. 10 rows for each ape).

variable description
apeID Ape's Name (all names are chosen to be unique)
age Age (in years) at assessment
species Species (chimp v orangutan)
HiP Happiness in Primate Scale (range 1 to 18)
timepoint Study visit (1 to 10) 
df <- read_csv("https://uoepsy.github.io/data/midlife_ape.csv")

# add polynomials
df <- df |> 
  mutate(
    poly1 = poly(timepoint,2,raw=F)[,1],
    poly2 = poly(timepoint,2,raw=F)[,2]
  )

mod1 = lmer(HiP ~ 1 + (poly1 + poly2) * species +
            (1 + poly1 + poly2 | apeID), 
            data = df)

summary(mod1)

Researchers are interested in investigating whether, after accounting for effects of sentence length, rhythmic tapping of fingers aids memory recall. They recruited 40 participants. Each participant was tasked with studying and then recalling 10 randomly generated sentences between 1 and 14 words long. For 5 of these sentences, participants were asked to tap their fingers along with speaking the sentence in both the study period and in the recall period. For the remaining 5 sentences, participants were asked to sit still.

Data are available at https://uoepsy.github.io/data/memorytap.csv, and contains information on the length (in words) of each sentence, the condition (static vs tapping) under which it was studied and recalled, and whether the participant was correct in recalling it.

variable description
ppt Participant Identifier (n=40)
slength Number of words in sentence
condition Condition under which sentence is studied and recalled ('static' = sitting still, 'tap' = tapping fingers along to sentence)
correct Whether or not the sentence was correctly recalled 
# TODO ANALYSIS

Data are available at

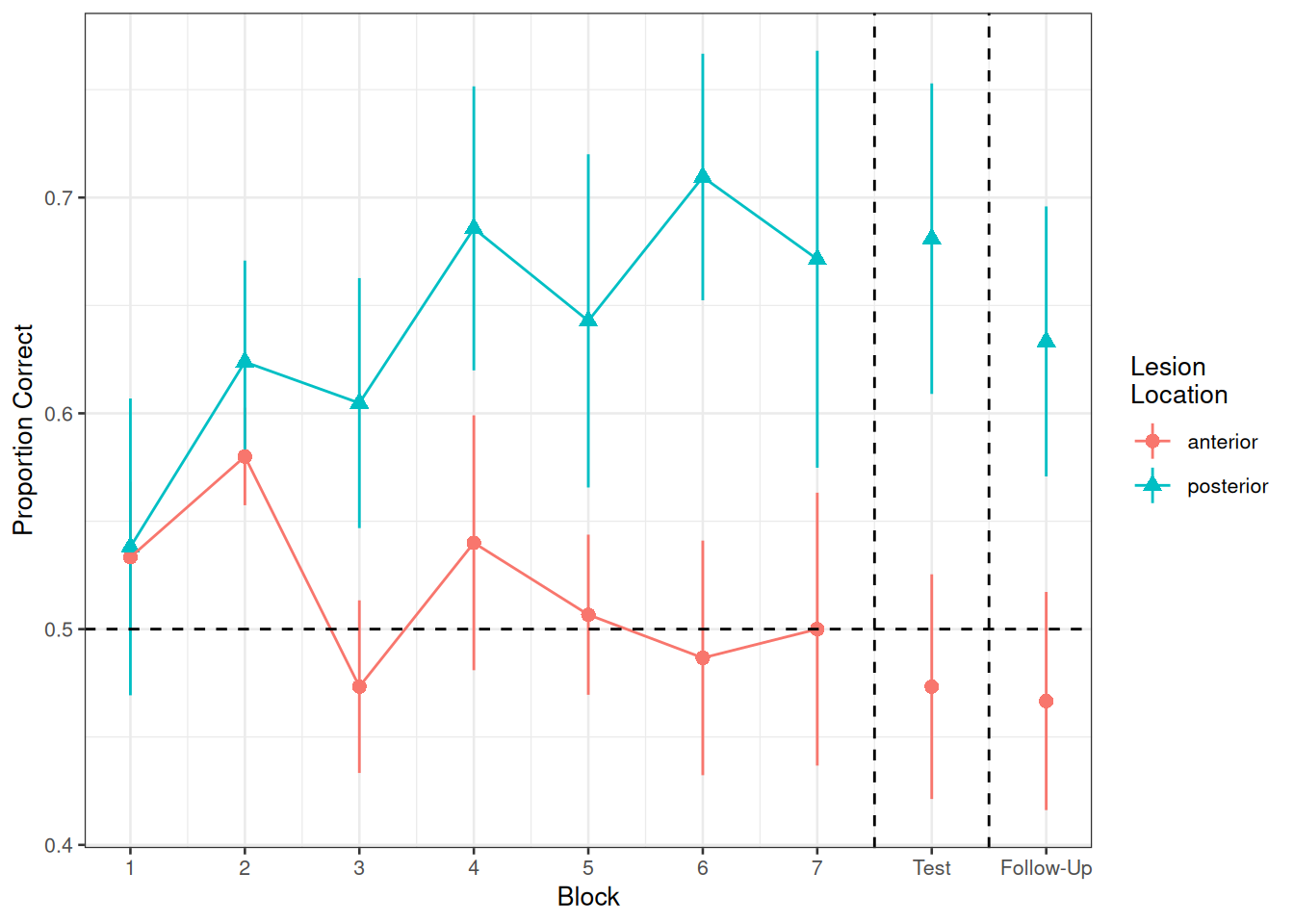
load(url("https://uoepsy.github.io/msmr/data/nwl.RData"))

In the nwl data set (accessed using the code above), participants with aphasia are separated into two groups based on the general location of their brain lesion: anterior vs. posterior. There is data on the numbers of correct and incorrect responses participants gave in each of a series of experimental blocks. There were 7 learning blocks, immediately followed by a test. Finally, participants also completed a follow-up test. Data were also collect from healthy controls.
Our broader research aim today is to compare the two lesion location groups (those with anterior vs. posterior lesions) with respect to their accuracy of responses over the course of the study.

Figure 1 shows the differences between lesion location groups in the average proportion of correct responses at each point in time (i.e., each block, test, and follow-up)

Figure 1: Differences between groups in the average proportion of correct responses at each block
variable description
group Whether participant is a stroke patient ('patient') or a healthy control ('control')
lesion_location Location of brain lesion: anterior vs posterior
block Experimental block (1-9). Blocks 1-7 were learning blocks, immediately followed by a test in block 8. Block 9 was a follow-up test at a later point
PropCorrect Proportion of 30 responses in a given block that the participant got correct
NumCorrect Number of responses (out of 30) in a given block that the participant got correct
NumError Number of responses (out of 30) in a given block that the participant got incorrect
ID Participant Identifier
Phase Experimental phase, corresponding to experimental block(s): 'Learning', 'Immediate','Follow-up' 
# TODO ANALYSIS

An experiment was run to conceptually replicate “test-enhanced learning” (Roediger & Karpicke, 2006): two groups of 25 participants were presented with material to learn. One group studied the material twice (StudyStudy), the other group studied the material once then did a test (StudyTest). Recall was tested immediately (one minute) after the learning session and one week later. The recall tests were composed of 175 items identified by a keyword (Test_word).

The critical (replication) prediction is that the StudyStudy group perform better on the immediate test, but the StudyTest group will retain the material better and thus perform better on the 1-week follow-up test.

We have two options for how we measure “test performance”:

  1. The time taken to correctly recall a given word.
  2. Whether or not a given word was correctly recalled

The following code loads the data into your R environment by creating a variable called tel:

load(url("https://uoepsy.github.io/data/testenhancedlearning.RData"))
variable description
Subject_ID Unique Participant Identifier
Group Group denoting whether the participant studied the material twice (StudyStudy), or studied it once then did a test (StudyTest)
Delay Time of recall test ('min' = Immediate, 'week' = One week later)
Test_word Word being recalled (175 different test words)
Correct Whether or not the word was correctly recalled
Rtime Time to recall word (milliseconds) 
# TODO ANALYSIS

The “Trolley Problem” is a thought experiment in moral philosophy that asks you to decide whether or not to pull a lever to divert a trolley. Pulling the lever changes the trolley direction from hitting 5 people to a track on which it will hit one person.

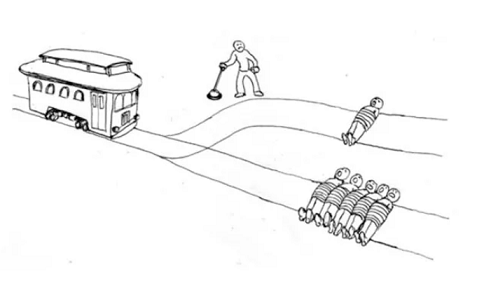
Previous research has found that the “framing” of the problem will influence the decisions people make:

positive frame neutral frame negative frame
5 people will be saved if you pull the lever; one person on another track will be saved if you do not pull the lever. All your actions are legal and understandable. Will you pull the lever? 5 people will be saved if you pull the lever, but another person will die. One people will be saved if you do not pull the lever, but 5 people will die. All your actions are legal and understandable. Will you pull the lever? One person will die if you pull the lever. 5 people will die if you do not pull the lever. All your actions are legal and understandable. Will you pull the lever?

We conducted a study to investigate whether the framing effects on moral judgements depends upon the stakes (i.e. the number of lives saved).

120 participants were recruited, and each gave answers to 12 versions of the thought experiment. For each participant, four versions followed each of the positive/neutral/negative framings described above, and for each framing, 2 would save 5 people and 2 would save 15 people.

Data are available at https://uoepsy.github.io/data/msmr_trolley.csv.

variable description
PID Participant ID
frame framing of the thought experiment (positive/neutral/negative
lives lives at stake in the thought experiment (5 or 15)
lever Whether or not the participant chose to pull the lever (1 = yes, 0 = no) 
# TODO ANALYSIS

Our primate researchers have been busy collecting more data. They have given a sample of Rhesus Macaques various problems to solve in order to receive treats. Troops of Macaques have a complex social structure, but adult monkeys tend can be loosely categorised as having either a “dominant” or “subordinate” status. The monkeys in our sample are either adolescent monkeys, subordinate adults, or dominant adults. Each monkey attempted various problems before they got bored/distracted/full of treats. Each problems were classed as either “easy” or “difficult”, and the researchers recorded whether or not the monkey solved each problem.

We’re interested in how the social status of monkeys is associated with the ability to solve problems.

Data are available at https://uoepsy.github.io/data/msmr_monkeystatus.csv.

variable description
status Social Status of monkey (adolescent, subordinate adult, or dominant adult)
difficulty Problem difficulty ('easy' vs 'difficult')
monkeyID Monkey Name
solved Whether or not the problem was successfully solved by the monkey 
df <- read_csv("https://uoepsy.github.io/data/msmr_monkeystatus.csv")

# relevel difficulty
df$difficulty <- factor(df$difficulty, 
                        levels=c("easy","difficult"))

mod1 <- glmer(solved ~ difficulty + status +
                (1 + difficulty | monkeyID), 
              family=binomial,
              data = df)

summary(mod1)